Using Big O notation to improve app performance
Using Big O notation to improve app performance
모던 소프트웨어에서 UX(user experience)은 굉장히 중요합니다. 그리고 성능은 좋은 UX의 중요한 요소입니다. 모던 소프트웨어는 모두 성능에 관한것이며, 이것은 사용자의 참여를 유지하거나 없앨 수 있는 능력에 영향을 미칩니다. 성능을 염두해 두고 디자인이 된 어플리케이션들은 성능을 생각하지 않은 어플리케이션들 보다 성공할 확률이 훨씬 더 높습니다.
흔한 오해는 간단한 코드 한 조각은 해를 끼치지 않는다는 것입니다. 반대로, 작은 코드 한 조각을 추가함으로써 생각했던것보다 더 나쁜 결과를 야기할 수 있다는 사실을 항상 염두해야합니다. 반면에 몇줄의 코드만을 추가함으로써 앱의 성능을 크게 향상시킬 수 있습니다.
이 글에서, 최신 어플리케이션의 성능을 향상시킬 수 있는 가장 쉬운 방법을 찾아보겠습니다: 빅오(Big O) 표기법을 사용해서 여러분이 만든 코드의 복잡도를 측정해보겠습니다.
What is Big O notation?
빅오 표기법은 알고리즘의 복잡도를 표현할 수 있는 수학적 과정입니다. 이 표기법은 컴퓨터 공학분야에서 굉장히 중요한 개념으로써 입력의 크기에 따라 알고리즘의 복잡도가 얼마나 증가하는지 설명해줍니다.
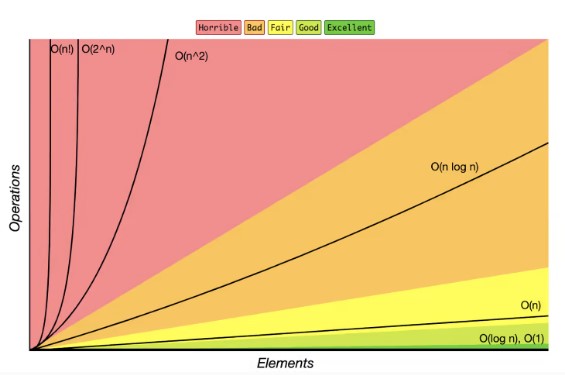 Image by Huyen Pham
Image by Huyen Pham
알고리즘의 복잡도를 측정하는 두가지 방법이 있습니다:
- 공간 복잡도(Space complexity)는 입력의 크기에 따라 알고리즘이 차지하는 정확한 공간의 양을 측정합니다. 공간 복잡도는 알고리즘에서 변수가 차지하는 공간을 계산함으로써 측정됩니다.
- 시간 복잡도(Time complexity)는 입력의 크기에 따라 알고리즘이 작동되는 정확한 시간의 양을 측정합니다. 시간 복잡도는 알고리즘의 실행이 끝나기 전에 실행해야 하는 단계의 수에 달려있습니다.
알고리즘의 시간 복잡도는 해당 알고리즘이 실행하는데 얼마나 걸리는지 측정함으로써 계산할 수 있습니다. 알고리즘의 복잡도를 계산하는데 있어서 세가지의 시나리오를 염두해 두어야 합니다.
- 가장 좋은 케이스 -> 알고리즘이 가장 빠른 시간에 완료됩니다. 가장 이상적인 솔루션입니다.
- 보통인 케이스 -> 알고리즘이 일반적이 시간에 완료됩니다.
- 나쁜 케이스 -> 알고리즘이 가장 느린 시간에 완료됩니다. 가장 최악의 솔루션입니다.
빅오 표기법을 사용하여 알고리즘의 복잡도를 계산할때, 항상 최악의 시나리오를 고려해야 합니다. 빅오 표기법(Big O notation)에서의 “O”는 함수의 순서를 나타내며 “n”은 입력값의 수를 나타냅니다.
O(1)
알고리즘의 가장 최상의 시간 복잡도는 일정한 시간(constant time)으로서 O(1)로도 알려져있습니다. 일정한 시간을 가지고 있는 알고리즘들은 항상 실행하는데 있어 같은 시간이 소요됩니다. 해당 알고리즘의 실행은 입력의 크기와는 무관합니다.
예를 들어, 두개의 숫자를 제곱하는 함수가 있다고 생각해봅시다.
const returnSquare = (num) => num * num;
returnSquare 함수는 실행하는데에 있어 같은 시간이 소요됩니다. 이것이 일정한 시간이 작동하는 방식이며, 입력의 크기와는 상관없이 동일한 시간 동안 실행이 되는 알고리즘 입니다.
이제 함수에서 배열을 받는다고 생각해봅시다. 배열의 크기와는 상관없이 우리는 배열의 첫번째 인자를 반환하고 싶습니다.
const getFirstItem = (arr) => arr[0];
getFirstItem 함수는 일정한 시간 복잡도를 가지고 있습니다. 왜냐하면 배열의 사이즈가 얼마나 커지든 실행하는데에 있어 걸리는 시간은 동일하니까요.
O(n)
가장 일반적인 시간 복잡도는 선형 시간 복잡도(linear time complexity)이며 O(n)으로 알려져 있습니다.
선형 시간 복잡도를 가진 알고리즘은 입력값의 크기에 따라 선형적으로 실행 시간이 걸립니다.
간단한 배열이 있고 특정한 요소를 찾기 위해 해당 배열을 순회한다고 생각해보세요:
const searchItem = (arr, item) => {
for (let i = 0; i < arr.length; i++) {
if (arr[i] === item) {
return item;
}
}
};
가장 최상의 시나리오는, 우리가 찾는 요소가 첫번째에 위치하고 있어 배열 전체를 순회할 필요가 없는것이죠. 가장 최악의 시나리오는 요소가 가장 마지막에 위치할 수도 있기에 배열 전체를 순회할 필요가 있다는 겁니다.
배열의 크기가 커질수록, 이 알고리즘의 시간 복잡도는 선형적으로 증가합니다. 알고리즘에서 루프(loop)를 볼때마다 해당 코드는 선형적인 시간 복잡도를 가지고 있는 알고리즘이라 추측할 수 있습니다.
O(log n)
여러분은 아마 학교에서 로그(logarithms)를 공부해 보셨을겁니다. 로그는 하나의 숫자에 도달하기 위해 얼마나 많은 숫자들이 곱해져야 하는지 결정하는 수학 공식입니다.
10개의 요소를 가지고 있는 배열이 있고 해당 배열을 순회할때 1초의 시간이 걸린다고 생각해봅시다. 해당 알고리즘의 시간 복잡도가 증가할수록, 20개의 요소를 순회하기 위해 2초가 걸릴것이고, 30개의 요소를 순회하기 위해 3초가 걸릴것이고 계속 이렇게 증가할겁니다.
O(log n) 알고리즘의 가장 좋은 예시는 이분 탐색법(binary search)입니다. 이분 탐색은 매 순회마다 배열을 반으로 나누어 정렬된 배열 안에서 특정 요소의 위치를 찾습니다.
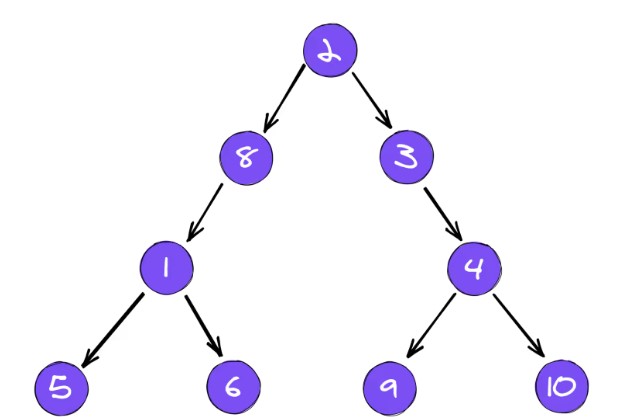 Image made using Excalidraw.
Image made using Excalidraw.
각 단계에서, 알고리즘은 문제의 크기를 반으로 줄입니다. 이진 검색 알고리즘을 예로 들자면 각 순회는 특정한 요소를 찾을때까지 배열을 나눕니다.
O(n!)
O(n!)는 알고리즘이 가질 수 있는 최악의 시간 복잡도를 나타냅니다. 코드를 작성할때, 팩토리얼 시간 복잡도(factorial time complexity)로 알려진 O(n!)의 시간 복잡도를 가지고 있는 코드를 작성하고 싶지는 않을겁니다.
O(!n)의 시간 복잡도를 가지고 있는 알고리즘은 생각하는것보다 무한대에 빨리 도달합니다. 팩토리얼 시간 복잡도에서는, 모든 입력한 값에다가 중첩 루프를 추가합니다.
이것이 가능하다는것을 알고있는것은 좋지만, 이런 시간 복잡도를 가진 코드는 아마 작성하기 싫을겁니다.
Conclusion
개발자들은 가독성을 기초로 하여 코드의 강도를 측정하는것을 좋아합니다. 가독성을 벤치마크로 사용하는데에는 아무런 문제는 없으나, 이것말고도 더 생각해야 하는 부분들이 있습니다.
성능은 모던 소프트웨어에서 굉장히 중요한 역할을 합니다. 하지만 성능 기준에 맞는 코드를 작성하는건 쉽지 않습니다. 작성된 코드의 복잡도 레벨을 알고 불필요한 것을 생성하지 않는것이 중요합니다.
빅오 표기법은 코드의 복잡도를 측정함으로써 성능 기준에 맞는 코드 작성을 도와줍니다. 이 개념은 많은 시간 동안 개발자들에게 매력적이고 성능이 좋은 소프트웨어를 만드는데 도움을 주었습니다.
원문: Using Big O notation to improve app performance by Leonardo Maldonado